

Blow reeds are riveted to the upper reed plate, draw reeds to the lower plate (holding your harp in the usual way). Normal blow notes are mainly generated by blow reeds, normal draws by draw reeds.

Imagine that you blow very gently into a harp channel - so gently, that there is no sound. The blow reed will all the same move a tiny little bit towards the reed plate, thereby tending to close the gap in the plate. The latter will also be true for the draw reed if one draws very gently. This common feature of both kinds of reeds will be described by the notion of a closing reed (see the table).
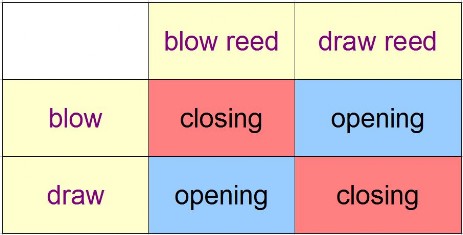
At the same time the second reed in the channel will respond reversed. Blowing very gently will cause the draw reed to move away from the reed plate, thus opening the gap a little bit more. The same is true for the blow reed if one is drawing. We will call the respective reed an opening reed (see table).
Playing frequency
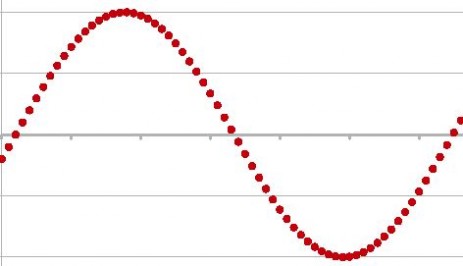
The red dots in the diagram depict the movement of the tip of an oscillating harmonica reed. Each red dot represents a snapshot of the reed tip. Looking from the left to the right and combining all snapshots to a movie (a GIF-animation), one can "see" the reed tip move up and down.
A sustained note with constant loudness implies reed movements up - down - up - down ... . A normal draw note on channel #4 of a C-harp corresponds to 600 repetitions of the pattern up-down-up (or down - up - down) per second.
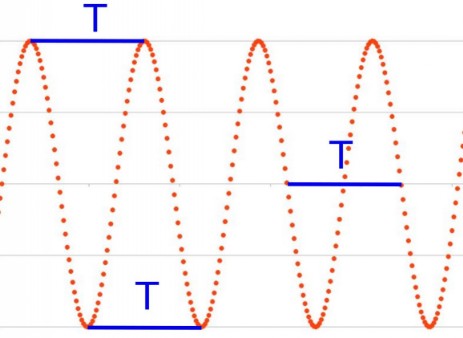
This amounts to a playing frequency f of 600 Hz (Hertz). One single oscillation lasts a time which is called oscillation period T. If there are 600 oscillations per second this oscillation period T will be the 600th part of one second, i. e. 1/600 seconds = 0.00167 seconds. Or, the other way round: If one oscillation lasts 0,00167 seconds, you will get the overall number of oscillations per second (i. e. the frequency = "how many Hertz") by dividing 1 (second) by 0.00167.
The audio was recorded with James Antakii's Turboharp ELX, a kind of pickup for blues harp reeds. So in the audio you "hear" directly the reed movement, not the sound radiated from the instrument.
Reed motion (D-reed)
Eigenfrequency
When you pluck a reed, you can hear its eigenfrequency (natural frequency) - the pitch of the fading plucking sound that you get displayed by a tuner.
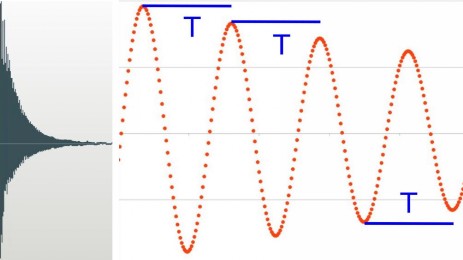

The reed tip still moves up and down, but the movement weakens from one "up" to the next. It still makes sense to talk about oscillation period and frequency (although the oscillation is not periodic in a literal sense - you may call it quasi-periodic). I have depicted a realistic waveform together with an idealized picture of tip motion. The recording lasted for 0.2 seconds, so there are about 120 (invisible) periods up-down-up. The decrease in the diagramm (red dots) is greatly exaggerated for clarity.
This audio clip (recorded with a microphone) presents the sound of a plucked D-reed (hole #4 of a C-harp). A tuning device will demonstrate that this natural frequency lies above the playing frequency recorded in the audio clip above.
Plucked D-reed
Now the last two audio clips are compared. You can hear that the normal draw note (recorded with help of the ELX) sounds noticeably lower than the plucked reed. The playing frequency of a normal note lies below the eigenfrequency of the closing reed.
Eigenfrequency - Playing frequency
Both reeds playing together
The following recordings prove that always both reeds in the channel of a blues harp oscillate - no matter what kind of note you play. All recordings were made with the help of a turpoharp ELX, so you hear directly the reed oscillations and not the radiated sound.
In the first three audio clips I am starting with a normal draw D on channel #4 of a C-harp and then bending it down as far as possible. You can first listen to the motion of both reeds (black), then exclusively to the blow reed (yellow), then only to the draw reed (magenta).
Both reeds
Blow reed
Draw reed
The recordings can only give a rough impression how strong the reeds actually oscillate. We are for example more sensitive for low volumes (we hear logarithmically, as experts say).
Measurements confirm: Normal notes are mainly generated by the closing reed, but the opening reed is also involved. If the closing reed moves 1mm up and down, the opening reed moves approximately 0.1mm.
Bending reduces the movement of the closing reed and augments the contribution of the opening reed. Bend notes with the lowest attainable pitch are mainly generated by the opening reed.
The next three audio clips present a normal draw B and successively lower draw bends on hole #3 of a C-harp. The lowest draw bend note Ab is mainly generated by the blow reed.
Normal draw and draw bend - both reeds
Normal draw and draw bend - blow reed
Normal draw and draw bend - draw reed
Next, there is a normal blow C and an overblow (near Eb) on hole #4 of a C-harp. The overblow is mainly generated by the draw (!) reed D.
.
Normal blow and overblow - both reeds
Normal blow and overblow - blow reed
Normal blow and overblow - draw reed
Finally, a normal blow E on hole #8 of a C-harp which is bent down. The lowest blow bend is nearly exclusively generated by the draw reed.
Normal blow and blow bend - both reeds
Normal blow and blow bend - blow reed
Normal blow and blow bend - draw reed
Single reeds
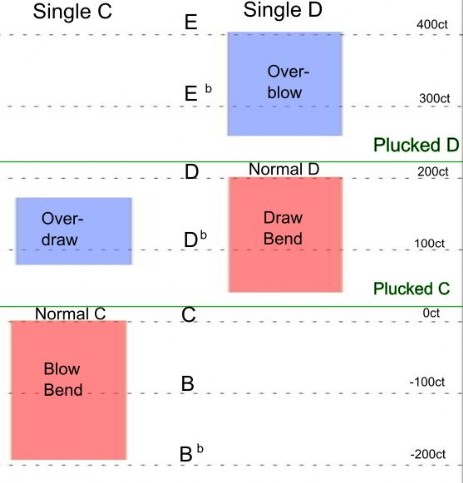
By taping the second reed in the channel, you can experiment with playing on single reeds. In addition to the normal blow and draw notes, both bends and overbends can be played on single reeds - be it blow or draw reeds.
The diagram shows in color all the notes I could play on channel #4 of a C-Harp. The horizontal dashed lines indicate the pitch. In addition to the corresponding note names, another representation perhaps familiar from tuning devices is used. The abbreviation "ct" means "cent" and comes from dividing a semitone interval into 100 parts (compare the division of meters into centimeters). Since we perceive pitches logarithmically, the cent scale is a so-called logarithmic scale. You don't need to understand the mathematics behind it - it's enough to know that the cent scale represents pitches as we perceive them. With such a scale, there is always a reference point "0ct" chosen (in the case of the tuner, it is the center of the scale). In the diagram, the playing frequency of the normal blow note C was chosen as the reference point. The normal draw note D is then two semitones away, i.e. 200ct.
The green lines mark the eigenfrequencies of the reeds (plucked C, plucked D). Even for normal notes, the playing frequencies are not simply equal to these eigenfrequencies. You can convince yourself of this by playing a normal blow or draw note and taking the instrument away from your mouth as quickly and as far as possible. The reeds continue to oscillate, gradually finding their eigenfrequency. The reverberating tone goes up slightly, but still audibly!
This behavior of the reeds has practical consequences for tuning blues harp reeds. Plucking the reeds and measuring the frequency with the tuner is not enough, you have to control the pitch for the assembled instrument. The volume between the cover and the reedplate, the volume of the comb and finally the vocal tract of the player all contribute a part to the pitch lowering.
This behavior of the reeds has practical consequences for tuning blues harp reeds. Plucking the reeds and measuring the frequency with the tuner is not enough, you have to control the pitch for the assembled instrument. The volume between the cover and the reedplate, the volume of the comb and finally the vocal tract of the player all contribute a part to the pitch lowering.
What can we learn from the diagram? Both reeds can be driven to oscillate by blowing as well as by drawing, and both blowing and drawing allow bends and overbends within a wide frequency range. Everything becomes clearer when you think of the division into closing and opening reeds. The closing reed is the blowing reed when blowing or the drawing reed when drawing. A closing reed allows a normal tone a quarter semitone below the eigenfrequency, which can be continuously bent downward. An opening reed allows an overbend a quarter semitone above the eigenfrequency, which can be continuously bent upwards: see the colors in the figure.
Result: We have not explained why closing and opening reeds behave the way they do. But we have gained an overview: The playing frequency for closing reeds is below their eigenfrequency, and the playing frequency for opening reeds is above their eigenfrequency. This gives us a unified description of, for example, the draw bends on the lower channels and the blow bends on the upper channels: If the closing reed in the channel has the higher eigenfrequency, the normal note it produces can be bent down.
Now, what distinguishes the blues harp from all other wind instruments is the idea of combining a closing reed and an opening reed in the same channel to form an overall system that can oscillate. We will also do this graphically in the next figure.
Two reeds
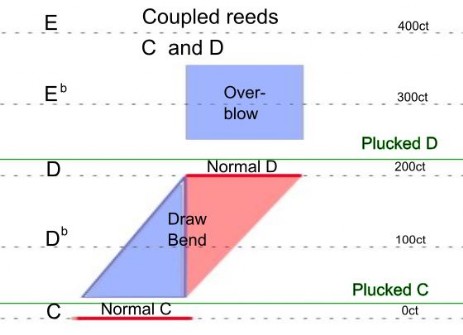
With
two reeds in one channel you can easily play a normal blow note and a
normal draw note with playing frequencies that would also come from a
single reed. On channel #4 you can continuously bend the draw note
down. The blow note cannot be bent, at least not with good tone and
not appreciably far down. Good players with good instrument
experience instead that the note seems to "pop" upwards and
an overblow sounds. This overblow can then be continuously bent
upward. Allowed playing frequencies of bendings and ended overblows
can also be directly targeted (for practitioners a life task).
In the illustration, red again stands for the closing reed and blue for the opening reed. The normal blow note C, for example, comes from the blow reed as closing reed and is therefore drawn in red. With the new understanding of closing and opening reeds, the normal draw note D is mainly produced by the closing draw reed D (but as demonstrated with the audios, the opening blow reed D oscillates as well). While this draw note is gradually bent downwards, the opening C reed starts to oscillate more and more, while the closing D reed oscillates less and less. At the lowest bend, almost only the opening reed oscillates. If you now remember the illustration with the playing frequencies of the single reeds, you could say: A drawbend with both reeds is a mix of a drawbend of the closing reed and an overdraw of the opening reed!
As already mentioned, there is no blowbend. The overblow comes almost exclusively from the opening D reed, which behaves like a single reed.
For any channel with differently tuned reeds, if the reed with the higher eigenfrequency is the closing reed (which depends on whether you blow or draw), the normal note it produces can be bent downwards. If the reed with the lower natural frequency is the closing reed, it can only produce a normal tone, while the other (necessarily opening) reed produces overbends.
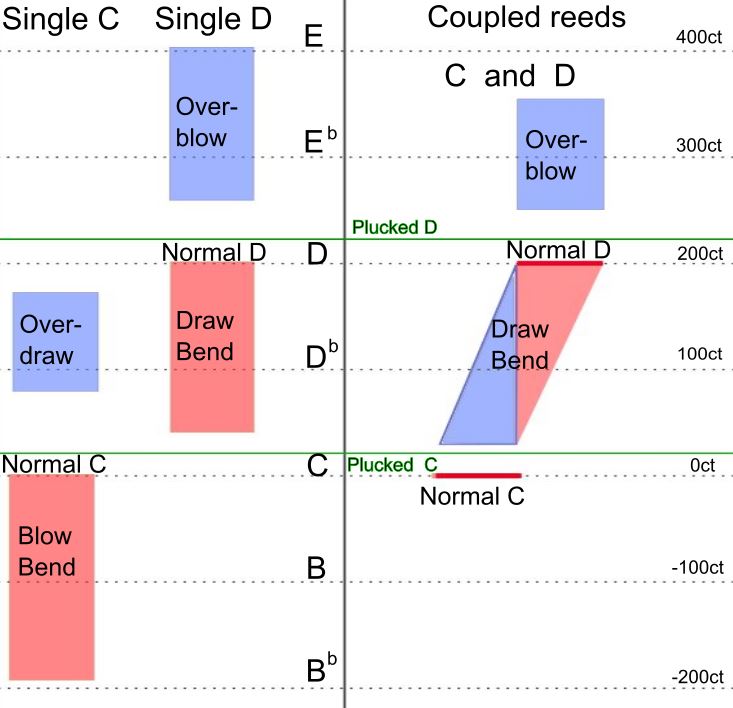
The following figure shows (again for channel #4 of a C-Harp) the behavior of single reeds and of both reeds together in comparison:
Self-excited oscillations
The reason we hear anything from the blues harp is that due to the pressure fluctuations in the chamber, accelerated air flows (jets) are formed through the gaps between the reedplate and the reeds. Due to the pressure fluctuations, the speed of the jet fluctuates. This in turn causes sound to be generated at the gaps. The blues harp can be compared to a siren, where a spinning perforated disc "chops" a fast jet. What we don't hear, by the way, are the pressure fluctuations in our vocal tract. Blues harp and instruments like saxophone or trumpet work completely differently here (in the case of the saxophone, a small part of the sound generated in the tube penetrates to the outside through openings).
Pressure fluctuations in the air flow and reed oscillations blow each other up when playing the blues harp. One says that the coupled system of airflow and reed(s) performs self-excited oscillations due to feedback. Feedback also exists as annoying feedback on stage, however, this is caused by an amplifier that is turned up too loud (for example, the harp amp). The self-excited oscillations in the blues harp (or also in the saxophone, trumpet or flute), on the other hand, do not involve an amplifier, so there is a different kind of "feedback".
How should we imagine the feedback between the airflow in the chamber and the two reeds? Does the airflow split in the direction of the reed (upwards) and in the direction of the draw reed (downwards), and does each partial flow communicate with "its" reed? The currently existing physical models for the blues harp assume that there is only one common airflow in the chamber, with the same pressure fluctuations acting on both reeds. This idea is supported by the fact that the pressure fluctuations in the air flow and the two reeds oscillate with common frequency (i.e., the playing frequency perceived from the outside) after only a very short time.
Cooperation during bending
Bending on the blues harp is in principle possible in the frequency range between the eigenfrequencies of the two reeds, if the reed with the higher tuning is the closing reed. In this range, each of the two individual reeds could perform self-excited oscillations in interplay with the pressure fluctuations in the air stream. Thus, in principle, the possibility of cooperation is given. In practice, it turns out that both reeds oscillate almost in parallel during bending. "Parallel" in this case means that the tips of the reeds move up and down synchronously.

The
illustration (cross-section through a blues harp chamber) shows that
parallelly oscillating reeds change the size of the slots between
reeds and reedplate in a comparable way. The size of the slots in
turn influences the airflow. Parallelly oscillating reeds thus
influence the airflow in a comparable way - they cooperate! Since
they influence the airflow together as they would do alone, they can
also together trigger the self-excited vibrations that they would
cause alone.
The overblow wins
For blow notes, the frequency ranges of the single reeds on channel #4 do not overlap. Since there is no playing frequency above its eigenfrequency for the blow reed as a single reed, it cannot participate cooperatively in the generation of an overblow. Conversely, the draw reed cannot actively contribute to a feedback process for either normal blow notes or blow bends.
Apparently, it is even the case that the reed " perturbs " the buildup of self-excited vibrations in the overblow region. In fact, playing overblows is much easier if you unscrew the covers of the harp and place a finger on the blow reed. If you want to opitimize your harp for overblows, reduce the reed gap of the blow reed and thus the part of the airflow that can be influenced by the blow reed.
Before misunderstandings arise: Both reeds also oscillate during blow notes; the reed not actively participating in the feedback process is also moved by the pressure fluctuations in the air stream, and the movements of this reed also have a feedback effect on the air stream - but not in such a way that self-excited oscillations could arise.
With a relaxed mouth position (embouchure), a normal blow note sounds. However, if you try to bend the blow note downward with the appropriate embouchure, you may hear little or nothing at all - or an overblow may occur. Self-excited blowbends triggered by the closing reed are obviously no longer possible as soon as the opening reed comes into play. In short: the overblow wins. It would be interesting to know why this is so …
